JEE 2018 :: Mathematics (2018) :: Solved questions (2018)

• Mathematics (2018) - Solved questions (2018)

Let s,t, r be non zero complex numbers and L be the set of solutions z=$ x + iy (x, y \in R$ ,i = $\sqrt{-1}$ ) of the equation $sz+i\bar{z}+r=0$ , where  $\bar{z}=x-iy$ , Then , which of the following statement (s) is (are) TRUE ?

Answer:

Explanation:

We have,  $sz+i\bar{z}+r=0$             ...........(i)

On taking conjugate,  $\bar{sz}+\bar{t}z+\bar{r}=0$         ..........(ii)

On solving Eqs.  (i)  and (ii) , we get

  z= $\frac{\bar{r}t-r\bar{s}}{\mid s\mid^{2}-\mid t\mid^{2}}$

(a) For unique solutions of z

${\mid s\mid^{2}-\mid t\mid^{2}}\neq 0 \Rightarrow \mid s \mid\neq \mid t\mid$

          It is true.

  (b)      If $\mid s \mid= \mid t\mid$, then $\bar{r}t-r\bar{s}$ may or may not be zero, So, z may have no solutions. 

 $\therefore $, L may be an empty set. It is false.

  (c)If elements of set L represents the line, then this line and given circle interset at maximum two-point . Hence, it is true

  (d)  In this case locus of z is a line, so L has infinite elements. Hence, it is true

Consider two straight lines, each of which is tangent to both the circle x²+ y²=(1/2) and the parabola y² =4x. Let these lines intersect at the point Q. Consider the ellipse whose center ia at the origin O(0,0) and whose semi-major axis is OQ. If the length of the minor  axis of this ellipse is $\sqrt{2}$ , then which of the following statement (s) is (are) TRUE?

Answer:

Explanation:

We  have, Equations of circle

$x^{2}+y^{2}=\frac{1}{2}$

 and equation of parabola

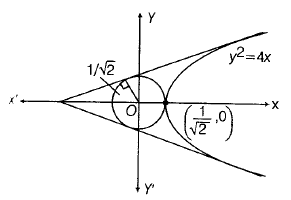
Let the equation of commpn tangent of parabola and circle is

          $y^{}=mx^{}+\frac{1}{m}$

  Since, radius of circle = $\frac{1}{\sqrt{2}}$

               $\frac{1}{\sqrt{2}}$  = $\mid\frac{0+0+\frac{1}{m}}{\sqrt{1+m^{2}}}\mid$

                      = m⁴+m²-m =0

                     = m ± 1

$\therefore$  Equation of common tangents are

                  y=x+1  and y=-x-1

 Intersection point of common tangent at Q(-1,0)

$\therefore$  equation of ellipse

                         $\frac{x^{2}}{1}+\frac{y^{2}}{1/2}=1$

where, a²=1 , b²=1/2

Now,

eccentricity $(e)=\sqrt{1-\frac{b^{2}}{a^{2}}}= \sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}}$

and length of latusrectum

               $\frac{2b^{2}}{a}=\frac{2(\frac{1}{2})}{1}=1$

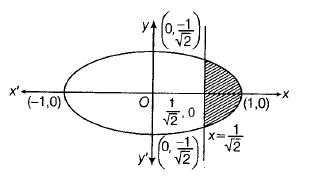
$\therefore$    Area of shadow region

                        = $2\int_{\frac{1}{\sqrt{2}}}^{1} \frac{1}{\sqrt{2}}\sqrt{1-x^{2}}dx$

                        = $\sqrt{2} [\frac{x}{2}\sqrt{1-x^{2}}+\frac{1}{2}\sin^{-1}x]_\frac{1}{\sqrt{2}}^1$

                        = $\sqrt{2}[(0+\frac{\pi}{4})-(\frac{1}{4}+\frac{\pi}{8})]$

                         =    $\sqrt{2}(\frac{\pi}{8}-\frac{1}{4})=\frac{\pi -2}{4\sqrt{2}}$

Let T be the line passing through the points P(-2,7) and Q(2,-5). Let F₁ be the set of all pairs of circles (S₁, S₂) such that T is tangent to S₁  at P and tangent to S₂ at Q , and also such that S₁ and S₂  touch each other at a point, say M. Let E₁ be the set representing  the locus of M as the pair (S₁ , S₂) varies in F₁.  Let the set of all straight line segments joining a pair of distinct points of E₁ and passing through the point R(1,1) be F2.  Let E₂ be the set of the mid-points of the line segments in the set F2. Then , which of the following statement (s) is (are) TRUE ?

Answer:

Explanation:

It is given that T is tangents to S₁ at P and S₂ at Q and S₁ and S₂ touch externally at M.

$\therefore$                             MN=NP=NQ

$\therefore$  Locus of M is a circle having PQ as its diameter of circle.

$\therefore$   Equation of circle,  (x-2)(x+2) + (y+5)(y-7)=0

 $\Rightarrow$  x² +y²-2y-39=0

 Hence, E₁ : x² +y² -2y-39=0, x≠ ± 2

 Locus of mid-point of chord (h,k) of the circle E₁ is xh+yk-(y+k)-39 = h² +k² -2k-39

$\Rightarrow$ xh+yk-y-k=h² +k² -2k

    Since the chord is passing through (1,1)

           Locus of midpoint of the chord (h,k) is 

                       h+k-1-k= h² +k² -2k

$\Rightarrow$   h² +k²-2k-h+1=0

 Locus is E₂ :  x² +y² -x-2y+1=0

 Now, after checking options , (a) and (d) are correct.

Let  $f:R\rightarrow R $ and $g :R\rightarrow R $ e two non-constant differentiable functions. If  $f'(x)=(e^{(f(x)-g(x)})g'(x)$ for all $x \in R$  and f(1)=g(2)=1, then which of the following statement(s) is (are) TRUE ?

Answer:

Explanation:

We have,

    $f'(x)=e^{(f(x)-g(x))}g'^{(x)}  \forall x \in R$

$\Rightarrow$        $f'(x)= \frac{e^{f(x)}}{e^{g(x)}}g'(x)$

$\Rightarrow$     $\frac{f'(x)}{e^{f(x)}}= \frac{g'(x)}{e^{g(x)}}$

$\Rightarrow$    $e^{-f(x)}f'(x)=e^{-g(x) }g'(x)$

  On integrating both sides, we get

   $e^{-f(x)}=e^{-g(x) }+c$

  At x=1,

  $e^{-f(1)}=e^{-g(1) }+c$

   $e^{-1}=e^{-g(1) }+c$    [ $\because$ f(1)= 1]  ......(i)

At x=2,

 $e^{-f(2)}=e^{-g(2) }+c$

$\Rightarrow$    $e^{-f(2)}=e^{-1}+C$  [   $\because$ g(2)= 1]    ..........(ii)

 From Eqs. (i)   and (ii)

 $e^{-f(2)}=2e^{-1}-e^{-g(1)}$              ............(iii)

$\Rightarrow$       $e^{-f(2)}>2e^{-1}$

 We know that , e^-x  is decreasing

   $\because$   $-f(2)<\log_{e}{2}-1$

                   $f(2)>1-\log_{e}{2}$

  $\Rightarrow$  $e^{-g(1)}+e^{-f(2)}=2e^{-1}$    [from Eq,(iii)]

$\Rightarrow$ $e^{-g(1)}<2e^{-1}$

    $-g(1)<\log_{e}{2}-1$

$\Rightarrow$     $g(1)>-\log_{e}{2}$                

Let P  be a point on the circle S with both coordinates being positive. Let the tangent to S  at P intersect the coordinate  axes at the points  M and N.  Then the mid -point of the line segment MN must lie on the curve

Answer:

Explanation:

We have, x² + y² =4

 Let $P(2\cos\theta,2\sin\theta)$  be a point on a circle.

  Tangent at P is  $2\cos\theta x+2\sin\theta y=4$

  = $x\cos\theta +y\sin\theta =2$

   $\therefore$     The coordinates at  $M(\frac{2}{\cos\theta},0)$ and $N(0, \frac{2}{\sin\theta})$

    Let (h,k) is mid-point of MN

  $\therefore$  $h= \frac{1}{\cos\theta}$   and   $k= \frac{1}{\sin\theta}$

 $\Rightarrow$ $\cos\theta =\frac{1}{h}$  and         

 $\sin\theta =\frac{1}{k}$

$\Rightarrow$        $\cos^{2}\theta +\sin^{2}\theta= \frac{1}{h^{2}}+\frac{1}{k^{2}}$

  $\Rightarrow$   $1= \frac{h^{2}+k^{2}}{h^{2}.k^{2}}$

$\Rightarrow$      $h^{2}+k^{2}= h^{2}.k^{2}$

  $\therefore$   Mid-point of MN lie on the curve

  $x^{2}+y^{2}=x^{2}y^{2}$

• Mathematics (2018) - Solved questions (2018)